[HackerRank] Simple Explanation: Flatland Space Stations

Introduction

Although the problem is categorized as “EASY” in terms of difficulty, I must admit that the solution didn’t immediately come to mind after reading the description. Nevertheless, I managed to find a straightforward and concise approach that is both easy to comprehend and implement.

I won’t explain the requirement here, so before reading the below explanation, I highly suggested that making sure we understand this problem’s description.

The challenge description can be found https://www.hackerrank.com/challenges/flatland-space-stations/problem

Explanation

The sample input is

5 2
0 4

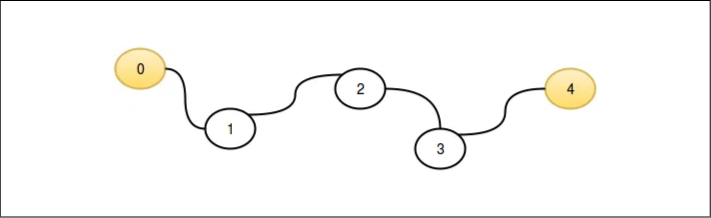
Okay. It means that there are 5 cities and 2 of them have a space station, and these two cities are respectively 0 and 4. The problem can be sketched as the above picture. It is quite straightforward.

The output as required is to find the maximum distance that an astronaut would need to travel to reach the nearest space station, that is, the maximum distance of one city to its nearest space station.

My tips:

1. Find the minimum distance of all cities to their nearest space station.
2. Find the maximum distance from the step 1 result.

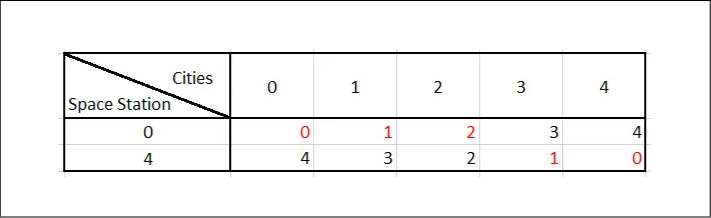
Let’s check the city 1 based on the above table. The distance between city One and space station Zero is 1, meanwhile, the distance between city One and space station Four is 3. Thus, the minimum distance of city One to its nearest space station is 1. If you understand this, the rest becomes easy. What we need to do is to find the maximum value from the minimum distance array as shown in the table(red digits). So 2 is the result.

Let’s try another sample, and draw the same table.

9 3
1 4 7

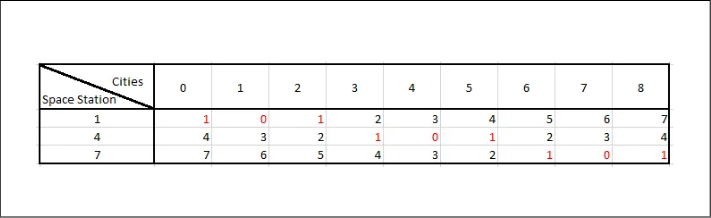
So the answer is obvious, right? Picking out the maximum value from a bunch of 0 and 1.

package main

import (
	"bufio"
	"fmt"
	"io"
	"math"
	"os"
	"strconv"
	"strings"
)

// Complete the flatlandSpaceStations function below.
func flatlandSpaceStations(n int32, c []int32) int32 {

	var (
		m   int32 = int32(len(c))
		i   int32 = 0
		max int32 = 0
	)

	if n == m {
		return 0
	}

	for i = 0; i < n; i++ {
		var min int32 = n  
	
		// Step 1:
		for _, station := range c {
			d := math.Abs(float64(i - station))
			if min > int32(d) {
				min = int32(d)
			}
		}
	
		// Step 2:
		if max < min {
			max = min
		}
	}

	return max
}

💡Line 27: variable indicates max distance between any of two cities won’t be longer than n.
💡Line 30-35: Find the minimum distance of all cities to their nearest space station, which was mentioned in the above tip 1.
💡Line 38-40: Find the maximum distance from the step 1 result, which was mentioned in the tip 2.

I decided to write this post here because I couldn’t find any easily understandable solution to this problem in the HackerRank discussion. Although the time complexity is O(n²), which is not particularly fast, the solution is clearer and successfully passed all the test cases.